Designing energy functions using
a linear programming technique
Obtaining constraints
on the Energy function
1) En
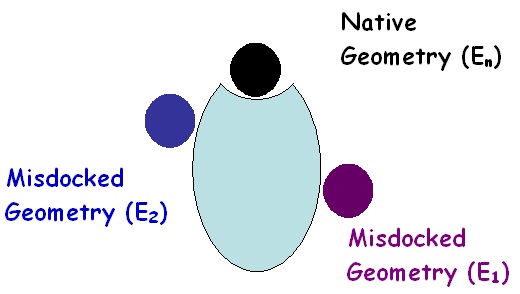
< E1
=> E1
- En
> 0 => DE1
> 0
2) En
< E2
=> E2
- En
> 0 => DE2
> 0
The basic requirement
from an energy function is, that the free energy of native complex
will be lower
than that of
any
misdocked geometry, for the same pair of proteins. Thus misdocked
complexes show how the energy function should not look like. This
information can be extracted in the form of constraints (inequalities) on
the energy function:
optimization of linear energy functions
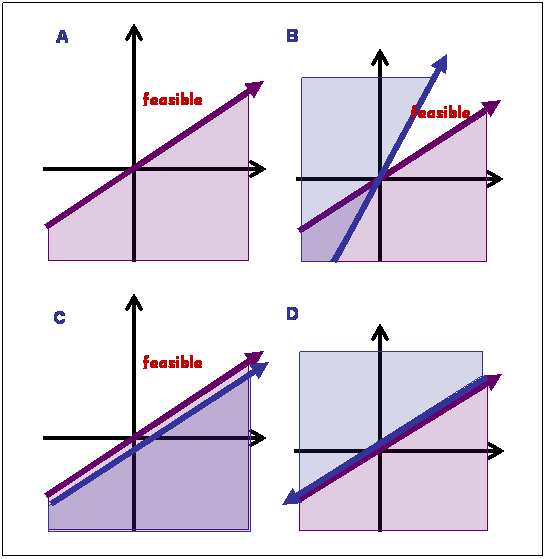
The choice of a linear
form for the energy function enable us to efficiently optimize the
parameters, such that, the energy of the native state will be lower than
that of every non native state. Each inequality divides the parameter
space into two regions (A):
allowed
(each point in the space represent a valid solution) and
forbidden.
A
given inequality may give rise to three outcomes: It may (B) reduce the
space allowed for the parameter set (most desirable), have no effect on
the allowed space (C), or impose an impossible condition (no solution
exist) (D). Optimization was done using the interior point algorithm
BPMPD
